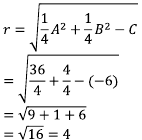Contoh Soal dan Pembahasan Persamaan Lingkaran Kelas 11

Primalangga-Contoh soal dan pembahasan persamaan lingkaran matematika kelas 11 SMA. bab yang akan dibahas diantaranya soal dan pembahasan persamaan garis singgung lingkaran, persamaan lingkaran melalui 2 titik.

Artikel awal ini membahas persamaan lingkaran dengan pusat titik (0, 0), titik (a, b) dan bentuk umum persamaan lingkaran,  garis singgung pada lingkaran dibahas pada artikel tersendiri.

contoh soal dan pembahasan persamaan lingkaran

Soal No. 1

Berikut lukisan sebuah lingkaran pada sumbu x dan sumbu y.

Tentukan:

a) koordinat titik pusat lingkaran

b) jari-jari lingkaran

c) persamaan lingkaran

Pembahasan

a) koordinat titik pusat lingkaran

dari gambar terlihat bahwa koordinat pusat lingkaran adalah (0, 0)

b) jari-jari lingkaran

Jari-jari lingkaran r = 5

c) persamaan lingkaran

lingkaran dengan pusat titik (0, 0) dengan jari-jari r akan memiliki persamaan dengan bentuk :

x² + y² = r²

sehingga

x² + y² = 5²

x² + y² = 25

Soal No. 2

Suatu lingkaran memiliki persamaan:

x² + y² = 144

Tentukan panjang diameter lingkaran tersebut!

Pembahasan

Lingkaran pusat di (0, 0) di atas memiliki jari-jari:

r = √144

= 12 cm.

Diameter lingkaran:

D = 2 r

= 24 cm.

Soal No. 3

Diberikan sebuah lingkaran seperti gambar berikut!

Tentukan:

a) koordinat titik pusat lingkaran

b) jari-jari lingkaran

c) persamaan lingkaran

Pembahasan

a) koordinat titik pusat lingkaran

pusat lingkaran terletak pada x = 5 dengan y = 6 sehingga koordinatnya adalah (5, 6)

b) jari-jari lingkaran

sesuai gambar diatas, jari-jari lingkaran adalah 5 − 2 = 3

c) persamaan lingkaran

lingkaran dengan titik pusat di (a, b) dengan jari-jari r akan memiliki persamaan berikut:

(x − a)² + (y − b)² = r²

dimana a = 5, dan b = 6

sehingga

(x − 5)² + (y − 6)² = 3²

(x − 5)² + (y − 6)² = 9

Soal No. 4

Persamaan suatu lingkaran adalah x² + y² − 8x + 4y − 5 = 0

Tentukan:

a) titik pusat lingkaran

b) jari-jari lingkaran

Pembahasan

Suatu lingkaran x² + y² + Ax + By + C = 0

akan memiliki titik pusat (−¹/₂A, −¹/₂ B) dan jari-jari r = √[¹/₄ A² + ¹/₄ B² −C] .

Dari persamaan lingkaran diatas nilai :

A = −8, B = 4 dan C = − 5

a) titik pusat (−¹/₂[−8], −¹/₂ [4]) = (4, −2)

b) jari-jari lingkaran r = √[¹/₄ (−8)² + ¹/₄ (4)² −(−5)] = √25 = 5

Soal No. 5

Jari-jari dan pusat lingkaran yang memiliki persamaan x² + y² + 4x − 6y − 12 = 0 adalah...

A. 5 dan (−2, 3)

B. 5 dan (2, −3)

C. 6 dan (−3, 2)

D. 6 dan (3, −2)

E. 7 dan (4, 3)

Pembahasan

x² + y² + 4x − 6y − 12 = 0

A = 4

B = −6

C = −12

Pusat:

Jari-jari:

Sehingga jari-jari dan pusatnya adalah 5 dan (−2, 3).

Soal No. 6

Lingkaran dengan persamaan 2x² + 2y² − ¹/₂ ax + 4y − 12 = 0 melalui titik (1, − 1). Diameter lingkaran tersebut adalah....

A. 2

B. 3

C. 4

D. 6

E. 8

Pembahasan

Masukkan titik (1, − 1) ke persamaan lingkaran untuk mendapatkan nilai a terlebih dahulu:

Jadi persamaan lingkarannya sebenarnya adalah

Jari-jarinya:

Diameternya adalah 2 × 4 = 8

Soal No. 7

Diberikan persamaan lingkaran:

x² + y² −4x + 2y − 4 = 0.

Titik A memiliki koordinat (2, 1). Tentukan posisi titik tersebut, apakah di dalam lingkaran, di luar lingkaran atau pada lingkaran!

Pembahasan

Masukkan koordinat A ke persamaan lingkarannya:

Titik A (2, 1)

x = 2

y = 1

x² + y² −4x + 2y − 4

= (2)² + (1)² −4(2) + 2(1) − 4

= 4 + 1 − 8 + 2 − 4

= −5

Hasilnya lebih kecil dari 0, sehingga titik A berada di dalam lingkaran.

Aturan selengkapnya:

Hasil < 0 , titik di dalam lingkaran

Hasil > 0 , titik akan berada di luar lingkaran.

Hasil = 0, maka titik berada pada lingkaran.

Soal No. 8

Diberikan persamaan lingkaran:

(x − 2)² + (x + 1)² = 9

Titik B memiliki koordinat (5, − 1).

Tentukan posisi titik B apakah berada di dalam, luar atau pada lingkaran!

Pembahasan

Untuk bentuk persamaan lingkaran bentuk (x − a)² + (x − b)² = r², kedudukan titik terhadap lingkarannya sebagai berikut:

Di dalam lingkaran untuk (x − a)² + (x − b)² < r²

Di luar lingkaran untuk (x − a)² + (x − b)² > r²

Pada lingkaran untuk (x − a)² + (x − b)² = r²

Masukkan koordinat B ke persamaan lingkarannya, lihat hasilnya terhadap angka 9, lebih besar, lebih kecil ataukah sama.

B (5, − 1)

x = 5

y = − 1

(x − 2)² + (x + 1)²

= (5 − 2)² + (−1 + 1)²

= 9

Hasilnya sama, jadi titik B berada pada lingkaran.

Soal No. 9

Diberikan persamaan lingkaran:

(x − 2)² + (x + 1)² = 9

Titik C memiliki koordinat (3, 4).

Tentukan jarak titik C dari pusat lingkaran!

Pembahasan

Persamaan lingkarannya,

(x − a)² + (x − b)² = r²

(x − 2)² + (x + 1)² = 9

Pusat lingkaran ini adalah,

P (a, b)

= (2, − 1)

Jarak titik C (3, 4) ke pusat P (2, − 1) ditentukan dengan rumus jarak antara dua titik:

Hasilnya

Terbalik angkanya hasilnya sama juga

Soal No. 10

Diberikan persamaan lingkaran sebagai berikut:

x² + y² −2x + 4y + 1 = 0

Jika pusat lingkaran adalah P(a, b) maka nilai dari 10a − 5b =....

A. −10

B. −5

C. 5

D. 10

E. 20

Pembahasan

x² + y² −2x + 4y + 1 = 0

Pusatnya adalah

P (−¹/₂[−2], −¹/₂ [4])

= (1, −2)

Jadi a = 1 dan b = − 2.

10a − 5b =....

10(1) − 5(−2) = 10 + 10 = 20

Soal No. 11 

Lingkaran yang persamaannya x² + y² − Ax − 10y + 4 = 0 menyinggung sumbu x. Nilai A yang memenuhi adalah...

A. − 2 dan 2

B. − 4 dan 4

C. − 5 dan 5

D. − 6 dan 6

E. − 9 dan 9

Pembahasan

Cara Pertama:

Lingkarannya menyinggung sumbu x, sehingga jari-jari lingkarannya akan sama dengan nilai positif dari ordinat titik pusatnya atau

Sehingga jari-jari lingkaran x² + y² − Ax − 10y + 4 = 0 adalah r = 10/2 = 5.

Dari rumus jari-jari lingkaran yang telah dihilangkan tanda akarnya:

Cara kedua:

Lingkaran yang persamaannya x² + y² − Ax − 10y + 4 = 0 menyinggung sumbu x. Artinya saat menyinggung sumbu x nilai y = 0. Masukkan ke persamaan, y diisi nol,

Terbentuk persamaan kuadrat, syaratnya menyinggung nilai diskrimanan sama dengan nol (D = 0), ingat D = b²− 4ac di materi persamaan kuadrat. Sehingga

Soal No. 12 

Persamaan lingkaran dengan pusat P(3, 1) dan menyinggung garis 3x + 4y + 7 = 0 adalah.....

A. x² + y² − 6x − 2y + 6 = 0

B. x² + y² − 6x − 2y + 9 = 0

C. x² + y² − 6x − 2y − 6 = 0

D. x² + y² + 6x − 2y + 6 = 0

E. x² + y² + 6x + 2y − 6 = 0

(Persamaan Lingkaran - UAN 2006)

Pembahasan

Kuncinya adalah mengetahui berapa jari-jari lingkaran terlebih dahulu. Baik diketahui dulu rumus untuk menentukan jarak suatu titik ke suatu garis.

Dalam kasus ini jari-jari lingkarannya sama dengan jarak titik ke garis, karena garisnya menyinggung lingkaran.

Jarak titik P(3, 1) ke garis x + 4y + 7 = 0 adalah

Dengan demikian jari-jari lingkarannya r = d = 4.

Tinggal membuat persamaan lingkarannya, pusatnya di titik (3, 1) dengan jari-jari 4

Soal No. 13

Jari-jari lingkaran pada gambar di bawah ini adalah...

A √3

B. 3

C. √13

D. 3√3

E. √37

(Lingkaran - Ebtanas 1996)

Soal No. 14

Tentukan persamaan garis singgung untuk lingkaran x² + y² = 29 yang melalui titik (5, − 2).

Pembahasan

Titik (5, − 2) terletak pada lingkaran dan sekaligus menjadi titik singgungnya, karena 5² + (−2)² = 25 + 4 = 29

Persamaan garis singgung lingkaran x² + y² = r² jika diketahui titik singgungnya adalah:

x₁x + y₁y = r²

5x + (−2)y = 29

5x − 2y = 29

Soal No. 15

Tentukan persamaan garis singgung untuk lingkaran x² + y² = 13 yang melalui titik:

a) (3, −2)

b) (3, 2)

Pembahasan

Tipe soal masih seperti nomor 14. Titik (3, − 2) dan titik (3, 2) sama-sama berada pada lingkaran x² + y² = 13 sehingga persamaan garis singgungnya masing-masing adalah:

a) x₁x + y₁y = r²

3x − 2y = 13

b) x₁x + y₁y = r²

3x + 2y = 13

Sekian dulu tengang Contoh soal dan pembahasan persamaan lingkaran matematika kelas 11 SMA. untuk pembahasan yang lebih lengkap akan di bahasa pada artikel selanjutnya. jangan lupa untuk mengunjungi artike lainnya.

.

NEXT PAGE >> 1 2 3